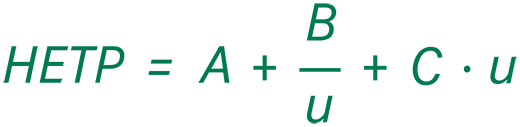由连接泵诱导的流体流动在层析分离中起着至关重要的作用。当然这种流动因层析柱和填料而异。然而,这并不意味着必须逐个计算流动模式才能成功地预测层析工艺。
流动模式在空间上是三维性的。层析流体动力学 (CFD) 模型在空间上也应该是三维的。但是,由于以下原因,3D 模型处理起来极其复杂:
- 分析填充床的精确几何结构(包括裂缝和外水体积)的实验工作量非常大。
- 模拟 3D 模型所需的计算能力随着网格细化的立方体而增长,且需求迅速变得巨大。
- 选择用于模拟特定层析应用的模型复杂性甚至可能不会显示 3D 效果。
Van Deemter:从 3D 模型到 1D 模型
好消息是,成功预测层析分离工艺不需要 3D CFD 模拟。实际上,层析柱的性能通过一个参数就可以充分地描述,即理论塔板高度 (HETP)。Van Deemter 方程将 HETP 与导致层析柱内峰展宽的不同影响因素关联起来:
- U—线性流速
- A—涡流扩散
- B—轴向扩散
- C—间隙体积、孔体积和固定相内部之间的传质。
层析柱的物理原理
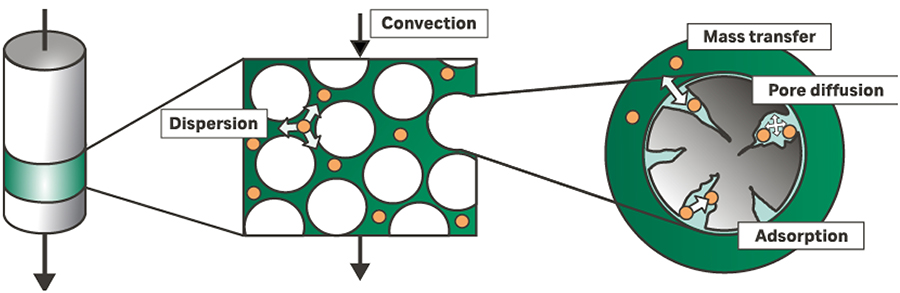
机理层析模型基于层析柱中发生的物理和生化现象的数学描述。图 1 描述了层析柱内的基本驱动机制,其中扩散结合了 Van Deemter 方程中的涡流扩散和轴向扩散。
图 1. 层析柱的基本原理。
对流
对流由连接的泵诱导发生。泵送速度越高,层析柱内的对流越大。具体来说,就是线性流速(单位时间的距离)随着横截面积的增大而减小。因此,间隙速度与管的直径成反比。
影响线性流速的另一个因素是颗粒床或膜的孔隙率。由于流动时必须围绕着静止颗粒或穿过膜,因此只有一小部分柱体积可用于流动。这种流动当然会大于诱导的流速,并与孔隙率成反比。
轴向扩散
分散利用 Van Deemter 方程中的两个量来考虑随机分子扩散和导致湍流的非理想流动模式。层析图上的结果是峰展宽,利用描述层析柱扩散的菲克第一定律建模形成。在运行期间流量变化较大的情况下,菲克扩散系数可以根据 Van Deemter 方程分为常数部分和流速相关部分。与对流效应相比,分散对层析图形状的影响更大。
膜传质
虽然轴向扩散考虑了 Van Deemter 方程中的两个效应,但其余量在建模时需要单独考虑膜传质和孔隙扩散。足够小的组分可以通过颗粒的滞止液膜进入颗粒孔隙体积内的流动相。通过膜向吸附剂表面的传质取决于颗粒和分子的特性以及浓度梯度。膜传质还会影响峰展宽。传质缓慢导致一些分子绕过颗粒而不进入孔隙。因为向间隙体积的传质同样缓慢,因而其他分子在孔隙中停留的时间更长。这种不同的行为加重了峰拖尾。
孔隙扩散
一旦组分进入颗粒的孔隙,其运动主要受扩散支配。液体中的扩散同样通过菲克扩散进行描述。孔隙扩散系数取决于固定相和流动相以及分子的特性。还有一种可以增强观测扩散的效应,那就是固定相表面上的扩散。这种扩散可以同时或单独发生。通过表面扩散,分子被吸附并在表面上灵活移动。由于热力学相互作用通常强于扩散效应,表面扩散常常被忽略或归入孔隙扩散系数中。
吸附
最终,组分可以吸附到颗粒的内表面上。有关蛋白质吸附的详细描述,请参阅等温线模型章节。
从物理原理到机理模型
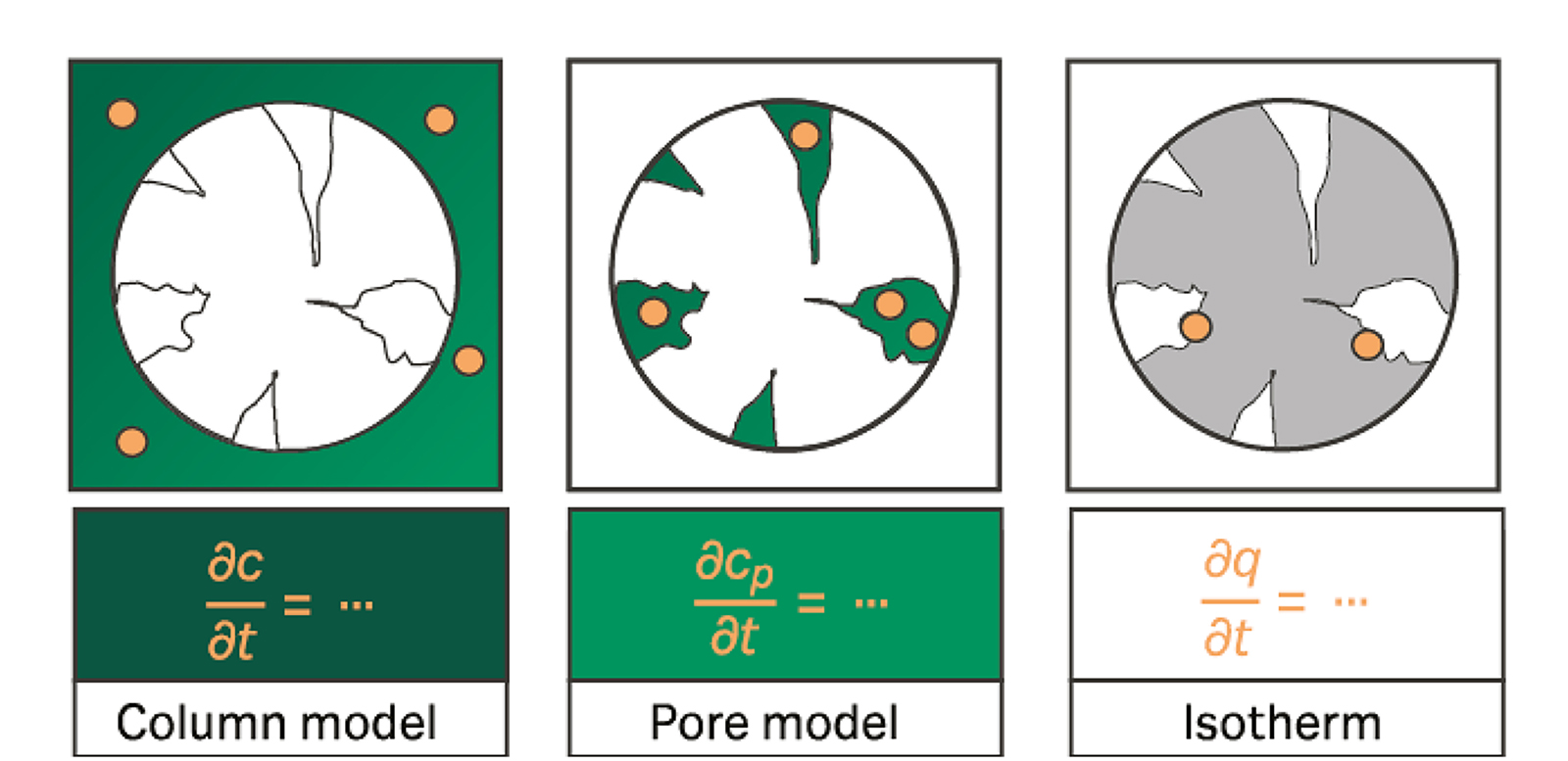
可以利用多种模型对液相层析进行数学描述。机理模型捕捉以下过程中的分子浓度变化:从流动相的间隙体积到流动相的孔隙体积,最后到固定相体积。
层析工艺的机理模型结合了以下模型方程:一个关于层析柱效应的模型方程(层析柱模型)、一个考虑小球孔隙内的流动相的模型方程(孔隙模型)和一种处理吸附过程的模型方程(等温线模型)。文献中描述了各种模型,它们的区别在于考虑的单独的物理效应数量不同。
平衡分散模型
平衡分散模型是一个非常基本的层析柱模型,它包括对流和分散的影响,用于描述流动相中的浓度传输。未明确考虑潜在微孔体积中的额外流体。层析柱横截面中的整个流体处于平衡状态。因此,该模型不适用于具有微孔体积的物料,如膜和整体柱或具有快速传质特性的颗粒。
传输分散模型和集总速率模型
与平衡分散模型一样,该模型利用对流和分散来描述间隙体积中的浓度传输。此外,孔隙内的流体体积浓度可能与外部不同。分子以有限的速率在体积之间传输。然而,由于未考虑孔隙扩散的影响,因此仅计算孔隙中的平均浓度。集总传质系数描述的是这两种效应的组合。
注:不同的教科书使用的上述术语的含义不同。
一般性速率模型
一般性速率模型是最详细、精度最高的模型。它适用于吸附具有复杂传质和吸附行为的溶质。一般性速率模型分开考虑传质和空隙扩散。另一个扩散子模型描述孔隙内液体从外部到中心的浓度传输。该模型包括膜传质系数和空隙扩散系数。由于现代层析填料的孔隙易于穿透,因此膜传质系数的影响通常小于空隙扩散参数。扩散模型采用球形小球。因此,空隙近似为圆锥形。这导致在小球中心附近发生快速的不对称扩散,而与外部方向相比,小球中心附近保留的体积较少。